
$0 \le x \le 2$에서 함수 $f(x)=-2x^2 -4kx -2k^2 +k+1$의
최댓값이 $0$이 되도록 하는 모든 실수 $k$의 값의 합을 구하여라.
먼저 이차함수 $f(x)$를 정리하면
$f(x)=-2x^2 -4kx -2k^2 +k+1$
$~~~~~~~=-2(x^2 +2kx) -2k^2 +k+2$
$~~~~~~~=-2(x+k)^2 +k+2$
$f(x)$의 대칭축의 방정식은 $x=-k$이고
$f(x)$는 위로 볼록의 그래프이므로
대칭축과의 거리가 가까울수록
대응되는 $y$좌표가 높다.
따라서 최댓값이 달라지는 경우는 다음 세 가지로 생각 할 수 있다.

빨간색은 범위 $0 \le x \le 2$의 구간을 나타낸다.
① $-k \le 0$ $(k \ge 0)$ 인 경우

$x=-k$와 $x=0$사이의 거리가 $x=2$사이의 거리보다 가깝다.
따라서 $0 \le x \le 2$에서 $f(x)$는 $x=0$일 때 최대
$f(0)=-2k^2 +k+1=0$
$2k^2 -k-1=0$
따라서 $k=1$ 또는 $k=- {1 \over 2}$
$ \therefore $ 범위를 만족하는 $k=1$
② $0<-k \le 2 ~~ (-2 \le k <0 ) $ 인 경우
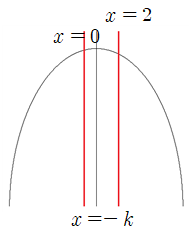
$0 \le x \le 2$에서 $f(x)$는 $x=-k$일 때 최대
따라서 $f(-k)=-2k^2 +4k^2 -2k^2 +k+1=0$
$k=-1$
$ \therefore ~~k=-1$
③ $-k>2~~(k<-2)$ 인 경우
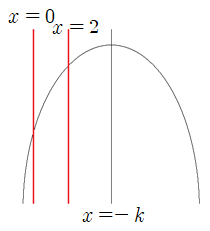
$x=-k$와 $x=2$사이의 거리가 $x=0$사이의 거리보다 가깝다.
따라서 $0 \le x \le 2$에서 $f(x)$는 $x=2$일 때 최대
$f(2)=-8-8k-2k^2 +k+1=0$
$2k^2 +7k+7=0$
위 식을 만족하는 실수 $k$의 값은 없으므로
만족하는 $k$값은 없다.
$ \therefore $ ①, ②, ③에서 모든 실수 $k$의 값의 합은 $1+(-1)=0$
아래 연습문제를 남기니 익혀보기 바란다.
'수학 > 수상' 카테고리의 다른 글
| 고차방정식 - 오메가 (5) | 2021.03.15 |
|---|---|
| 고차방정식 - 상반방정식 (2) | 2021.03.15 |
| 이차방정식과 이차함수2 (0) | 2021.03.12 |
| 이차방정식과 이차함수 (0) | 2021.03.11 |
| 이차방정식2 (4) | 2021.03.10 |