
삼차방정식 $x^3 -1=0$의 한 허근을 $\omega$라고 할 때,
다음을 $a \omega +b$(단, $a$, $b$는 실수)의 꼴로 나타내어라.
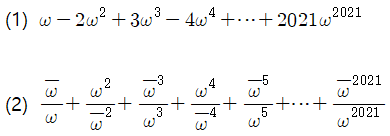
$\omega$는 읽을 때, 오메가라고 읽는다.
학생들이 많이 어려워하는 오메가 문제이다.
이런 유형의 문제는 항상 $6$가지를 먼저 구한다.
$x^3 -1 =(x-1)(x^2 +x+1)=0$
$x-1=0$ 또는 $x^2 +x+1=0$
$x^2 +x+1=0$은 허근을 가지므로 그 근이 $\omega$
또 $x^2 +x+1=0$ 은 계수가 모두 실수이므로
반드시 복소수의 켤레근을 가진다.
따라서 의 두 근은 $\omega$, ${\bar{\omega}}$ 이다.
따라서 $x^3 -1=0$의 세 근은
$x=1$, $\omega$, ${\bar{\omega}}$이다.
$x^3 -1=0$의 근이 $x=1$, $\omega$, ${\bar{\omega}}$이므로
① $\omega ^3 =1$
② ${\bar {\omega}} ^3 =1$
$x^2 +x+1=0$의 두 근은 $\omega$, ${\bar{\omega}}$
③ $\omega^2 + \omega +1=0$
④ ${\bar{\omega}}^2 +{\bar{\omega}} +1=0$
⑤ $\omega + {\bar{\omega}} =-1$
⑥ $\omega {\bar{\omega}}=1$
(1) $\omega -2 \omega^2 +3 \omega^3 -4 \omega^4 + \cdots + 2021 \omega^{2021}$
$\omega ^3 =1$이므로
$\omega = \omega^4 = \omega^7 = \cdots$
$\omega^2 = \omega^5 = \omega^8 = \cdots$
$\omega^3 = \omega^6 = \omega^9 = \cdots$
순환마디가 $3$개이다.
순환마디가 $3$개라고 가정하고
$3$개씩 나열해보자.
① $\omega -2 \omega^2 +3 \omega^3 = \omega -2 \omega^2 +3$
② $-4 \omega^4 +5 \omega^5 -6 \omega^6 = -4 \omega + 5 \omega^2 -6$
같지않다.
그러면 순환마디가 $6$개라고 가정하고
$6$개씩 나열해보자.
① $\omega -2 \omega^2 +3 \omega^3 -4 \omega^4 +5 \omega^5 -6 \omega^6$
$=\omega -2 \omega^2 +3 -4 \omega +5 \omega^2 -6 $
$=-3\omega +3 \omega^2 -3 =3( \omega^2 - \omega -1)$
$=3(- \omega -1- \omega -1)=-6( \omega +1)$
$( \because ~ \omega^2 +\omega +1=0$, $ \omega^2 =- \omega -1)$
② $7\omega^7 -8 \omega^8 +9 \omega^9 -10 \omega^{10} +11 \omega^{11} -12 \omega^{12}$
$=7\omega -8 \omega^2 +9 -10 \omega +11 \omega^2 -12 $
$=-3\omega +3 \omega^2 -3 =3( \omega^2 - \omega -1)$
$=3(- \omega -1- \omega -1)=-6( \omega +1)$
$\omega -2 \omega^2 +3 \omega^3 -4 \omega^4 +5 \omega^5 -6 \omega^6$
$=7\omega^7 -8 \omega^8 +9 \omega^9 -10 \omega^{10} +11 \omega^{11} -12 \omega^{12}$
$=-6( \omega +1)$
따라서 순환마디는 $6$개이다.
사실 $\omega$는 순환마디가 $3$개이고,
$1$, $-1$은 순환마디가 $2$개이므로
전체적으로 순환마디는 $6$개일 수 밖에 없다.
$2021=336 \times 6+5$
$\omega -2 \omega^2 +3 \omega^3 -4 \omega^4 + \cdots + 2021 \omega^{2021}$
$=-6( \omega +1) \times 336$
$~~~~~~~~~~+ 2017\omega^{2017} -2018 \omega^{2018}$
$~~~~~~~~~~~~~~~~~~~~~~+2019 \omega^{2019} -2020 \omega^{2020} +2021 \omega^{2021}$
$=-2016( \omega +1)$
$~~~~~~~~+ 2017\omega -2018 \omega^2 +2019 -2020 \omega +2021 \omega^2$
$=-2016( \omega +1)$$-3\omega +3 (-\omega -1)+2019$
$=-2016( \omega +1)$$-6\omega +2016$
$=-2022 \omega$

$\omega ^3 =1$이므로
$\omega = \omega^4 = \omega^7 = \cdots$
$\omega^2 = \omega^5 = \omega^8 = \cdots$
$\omega^3 = \omega^6 = \omega^9 = \cdots$
${\bar{\omega}} ^3 =1$이므로
${\bar{\omega}} = {\bar{\omega}}^4 = {\bar{\omega}}^7 = \cdots$
${\bar{\omega}}^2 = {\bar{\omega}}^5 = {\bar{\omega}}^8 = \cdots$
${\bar{\omega}}^3 = {\bar{\omega}}^6 = {\bar{\omega}}^9 = \cdots$
순환마디가 $3$개이다.
순환마디가 $3$개라고 가정하고
$3$개씩 나열해보자.

같지않다.
그러면 순환마디가 $6$개라고 가정하고
$6$개씩 나열해보자.
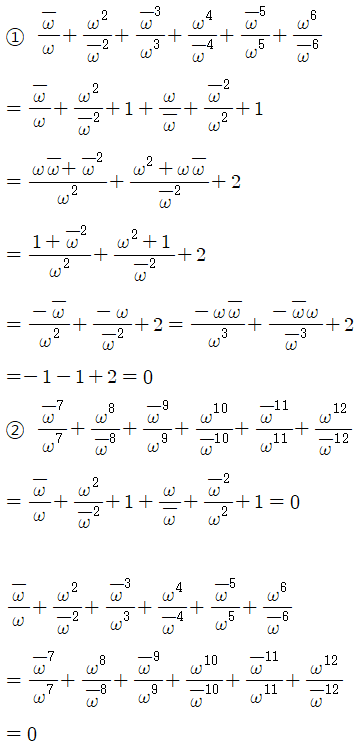
따라서 순환마디는 $6$개이다.
$2021=336 \times 6 +5$
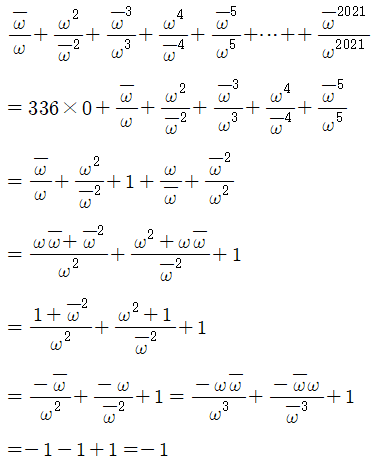
오메가 문제는 항상 $6$가지를 먼저 구하고 푼다.
$x^3 -1=0$의 한 허근이 $\omega$이면
① $\omega ^3 =1$
② ${\bar {\omega}} ^3 =1$
③ $\omega^2 + \omega +1=0$
④ ${\bar{\omega}}^2 +{\bar{\omega}} +1=0$
⑤ $\omega + {\bar{\omega}} =-1$
⑥ $\omega {\bar{\omega}}=1$
하지만 위의 $6$가지를 외워서 풀면 안된다.
주어진 식에 따라 계속 바뀐다.
예를들어
$x^3 -8=0$의 한 허근이 $\omega$이면
① $\omega ^3 =8$
② ${\bar {\omega}} ^3 =8$
$x^3 -8 =(x-2)(x^2 +2x+4)=0$
③ $\omega^2 + 2\omega +4=0$
④ ${\bar{\omega}}^2 +2{\bar{\omega}} +4=0$
⑤ $\omega + {\bar{\omega}} =-2$
⑥ $\omega {\bar{\omega}}=4$
아래 연습문제를 남기니 익혀보기 바란다.
'수학 > 수상' 카테고리의 다른 글
| 고차방정식 - 상반방정식 (2) | 2021.03.15 |
|---|---|
| 이차방정식과 이차함수3 (10) | 2021.03.12 |
| 이차방정식과 이차함수2 (0) | 2021.03.12 |
| 이차방정식과 이차함수 (0) | 2021.03.11 |
| 이차방정식2 (4) | 2021.03.10 |