
$x$에 관한 이차방정식 $x^2 -2(m-4)x+2m=0$의 근이
다음 조건을 만족하도록 실수 $m$의 값의 범위를 정하여라.
(1) 두 근이 모두 $3$보다 크다.
(2) 두 근이 모두 $3$보다 작다.
(3) $3$이 두 근 사이에 있다.
(1)두 근이 모두 $3$보다 크면,
$f(x)=x^2 -2(m-4)+2m$라 하자.
① 두 근을 가져야한다. → $D \ge 0$
중근인 경우도 두 근이라고 생각해야한다.
$x^2 -2(m-4)x+2m=0$의 두 근은
$f(x)=x^2 -2(m-4)+2m$의 두 $x$절편으로 생각 할 수 있다.
두 근을 $\alpha$, $\beta$라 하면 $\alpha + \beta =2(m-4)$
② 두 근이 모두 $3$보다 크면
$f(x)$의 두 $x$절편이 모두 $3$보다 크다.
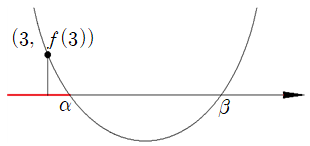
위 그래프처럼 되어야 하므로 $f(3)>0$
그런데 여기에는 문제가 있다.
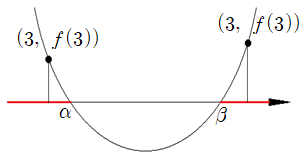
$f(x)>0$인 부분은 위처럼 두 군데이므로
$f(3)>0$이면 $(3,~f(3))$은 왼쪽, 오른쪽 모두 가능하다.
그러므로 $(3,~f(3))$을 왼쪽으로 정할 수 있는
조건이 추가 되어야한다.
따라서
③ 대칭축의 방정식$>3$ 즉, $ {{\alpha + \beta } \over 2} >3$

정리하면
① $D \ge 0$
② $f(3)>0$
③ $ {{\alpha + \beta} \over 2} =m-4 >3$
${D \over 4} =(m-4)^2 -2m \ge0$, $m^2 -10m+16 \ge0$
$(m-2)(m-8) \ge 0$
$m \ge 8$ 또는 $m \le 2$
$f(3)=9-6(m-4)+2m>0$
$-4m+33>0$, $m< {33 \over 4}$
$m-4>3$, $m>7$
세 조건의 공통범위를 구하면
$ \therefore ~~8 \le m < {33 \over 4}$
(2)두 근이 모두 보다 작으면,
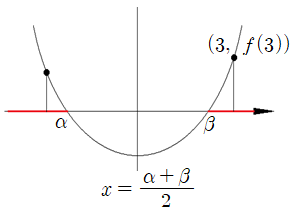
위 그림과 같으므로
마지막 조건만 바뀌면 된다.
① $D \ge 0$
② $f(3)>0$
③ $ {{\alpha + \beta} \over 2} =m-4 <3$
${D \over 4} =(m-4)^2 -2m \ge0$, $m^2 -10m+16 \ge0$
$(m-2)(m-8) \ge 0$
$m \ge 8$ 또는 $m \le 2$
$f(3)=9-6(m-4)+2m>0$
$-4m+33>0$, $m< {33 \over 4}$
$m-4<3$, $m<7$
세 조건의 공통범위를 구하면
$ \therefore ~~ m \le 2 $
(3) 두 근 사이에 3이 있으면

위 그래프와 같으므로
$f(3)<0$이면 된다.
① 판별식이 필요 없는 이유

$f(x)$의 그래프는 위 세 가지 중 하나인데
대응되는 $y$값이 음수가 있는 경우는 제일 왼쪽이므로
따라서 $f(3)<0$이면 반드시 $x$절편이 $2$개 생긴다.
② 대칭축의 방정식이 필요 없는 이유
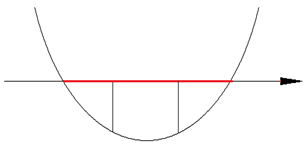
그래프에서 보듯이 $x=3$이
대칭축의 왼쪽이든 오른쪽이든 상관없다.
따라서 $f(3)<0$을 풀면
$f(3)=9-6(m-4)+2m<0$
$-4m+33<0$, $m> {33 \over 4}$
아래 연습문제를 남기니 익혀보기 바란다.